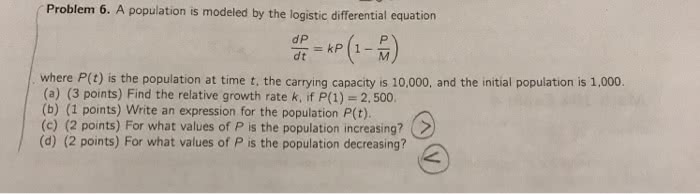MAT136H1 Lecture Notes - Relative Growth Rate, Partial Fraction Decomposition

20 views1 pages

ultramarineeel914

8 Apr 2013

School

Department

Course

Professor

For unlimited access to Class Notes, a Class+ subscription is required.

plummouse698 and 39596 others unlocked

MAT136H1 Full Course Notes

Verified Note

92 documents

Document Summary

If the given equation is not in this form, needs to be factored in order to determine and . The population follows after the equation, where is in years. Solution: given the equation, factor out the factor: ( ) ( Then comparing to the logistic differential equation form, ), the carrying capacity , and relative growth rate term: in order to find ( ), first ( ) needs to be established. Then ( : the population will reach 50% of its carrying capacity when: ( ) ( ) ; apply ln to both sides: its carrying capacity.

Related Questions

The logistic function in form of differential equation is given by,

where, P is population growth as function of time, ‘r’ is the growth rate and K is the carrying capacity.

If the carrying capacity is the also function of time K(t) and changing with time given as ,

How the population growth will follow the varying carrying capacity?

The population of the world was about 5.3 billion in 1990. Birth rates in the 1990s ranged from 35 to 40 million per year and death rates ranged from 15 to 20 million per year. Let's assume that the carrying capacity for world population is 120billion. (Assume that the difference in birth and death rates is 20 million/year = 0.02 billion/year.)

(a) Write the logistic differential equation for these data. (Because the initial population is small compared to the carrying capacity, you can take k to be an estimate of the initial relative growth rate. Let P be the population in billions and t be the time in years, where

t = 0

corresponds to 1990.)

dP/dt =

year 2100		P	=
year 2500		P	=

=

(b) Use the logistic model to estimate the world population in the year 2000. Compare with the actual population of 6.1 billion. (Round the answer to two decimal places.)
P =

(c) Use the logistic model to predict the world population in the years 2100 and 2500. (Round your answer to two decimal places.)

(d) What are your predictions if the carrying capacity is 60 billion? (Round your answers to two decimal places.)

year 2000	P	=
year 2100	P	=
year 2500	P	=

MAT136H1 Lecture Notes - Relative Growth Rate, Partial Fraction Decomposition

MAT136H1 Full Course Notes

Document Summary

Get access

Related Documents

MAT136H1 Lecture Notes - Relative Growth Rate, Logistic Function, Differential Equation

MAT136H1 Lecture 16: 8.5 Modelling with Differential Equations

MAT136H1 Lecture Notes - Product Rule, Linear Differential Equation, Integrating Factor

Related Questions