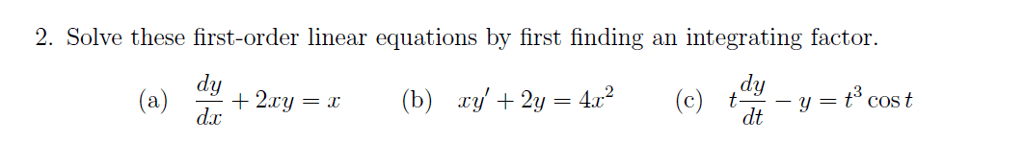MATH 310 Study Guide - Final Guide: Integrating Factor, Wronskian

• School: Simon Fraser University
• Department: Mathematics
• Course: MATH 310
• Professor: Sj Ruuth

Document Summary

Classi cation of des: order; linear vs. nonlinear; ordinary vs. partial; system of eqns vs. a single equation: chapter 2: 2. 1 integrating factors for 1st order linear des. 2. 5 autonomous equations and the phase line. 2. 3: modeling with rst order equations: chapter 3: 3. 1, 3. 3, 3. 4: solving ay(cid:48)(cid:48) + by(cid:48) + c = 0 via ar2 + br + c = 0 with roots r1 and r2: 3. 1: r1 (cid:54)= r2 real numbers: y(t) = c1er1t + c2er2t. 3. 3: r1, r2 = i : y(t) = c1e t cos( t) + c2e t sin( t) 3. 4: r1 = r2 r: y(t) = c1er1t + c2ter1t. 3. 7: application to mechanical & electrical vibrations. Mu(cid:48)(cid:48) + u(cid:48) + ku = f. Methods: 2. 1: integrating factor for 1st order linear equation: given y(cid:48) + p(t)y = g(t), (t) = e (cid:90) g dt. compute and solve.