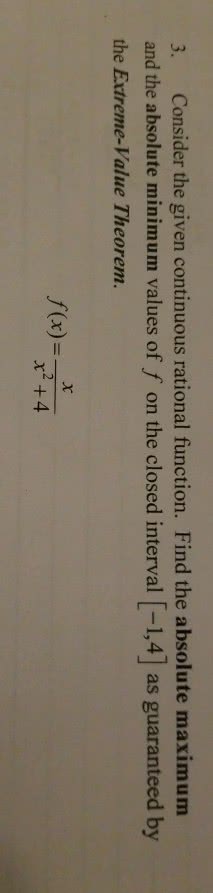MAT237Y1 Study Guide - Level Set, Wavelength-Dispersive X-Ray Spectroscopy, Compact Space
Document Summary
)}0,0{(\}1: (a) verify whether or not the following statements are correct. No marks for guessing. (i) [3 marks] if s int. R attains its absolute minimum value and its absolute maximum value on the set. , where il denotes the line segment in. )0,0( to the point on the circular arc y. By the extreme value theorem, continuous function is sure to attain its absolute if s is compact. minimum value and its absolute maximum value on the set. 1. (c) [5 marks] consider the area a of the parallelogram generated by the vectors u. To which non-zero component of the vectors u, v is the value of the area a most sensitive? (that is a small change of that component causes the biggest change of the value of a) Hence a small change of dx causes the largest change in a, and consequently a is most sensitive to the entry 2 of the vector u.